Measuring rainfall – it’s easy and difficult at the same time

This week we welcome long-time friend of GLOBE, Dr. Peggy LeMone, Chief Scientist for the GLOBE Program from 2003-2009, as our guest blogger. Dr. LeMone is currently working in the field of weather and cloud formation at the National Center for Atmospheric Research (NCAR).

Originally posted at http://spark.ucar.edu/blog/measuring-rainfall on September 23, 2013.

Dr. Peggy LeMone is an NCAR Senior Scientist who studies weather and cloud formation. For more information about her research, visit Peggy’s home page.

A guest post by NCAR scientist Peggy LeMone

The Boulder, Colorado area received huge amounts of rain in mid-September.  You also learned that rainfall amounts vary a lot. Which brings us to the questions – How do you measure rain?  And how accurate are the measurements?  Even though I have done weather research for many years, during this storm I was reminded how hard it is to measure rain accurately.

This is the story of my attempts to measure rain during the storm. It’s also about the many possible sources of error when making rain measurements – from old rain gauges to growing trees and even, possibly, inquisitive raccoons.

By Monday morning (September 16), I had measured over 16 inches, or 405 millimeters (mm), in our backyard rain gauge from the storm which began September 10.  The gauge is the same type the National Weather Service uses. It has a funnel that deposits rain into an inner tube with a smaller diameter (like this one), but bigger. The inner tube’s diameter is just small enough to make the depth of rain ten times what it would be in a gauge without the tube and funnel.  Thus, each inch in the tube is equivalent to 0.1 inches (a tenth of an inch) of rainfall.  This is equivalent to how the GLOBE rain gauge measures rain: the inner tube acts like a 10x magnifying glass for the area of the rain gauge.  This makes it easier to read accurately!

My gauge is old. I inherited it from a weather-observing neighbor who moved away.  The funnel and inner tube doesn’t quite fit, so, I leave the gauge open and then pour the rain into the inner tube using the funnel.

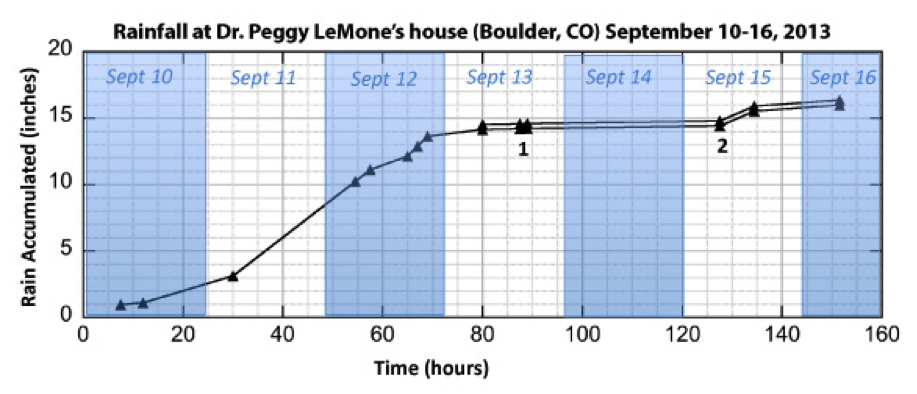
On the morning of September 12th, the gauge was so full and heavy, with over seven inches (178 mm) of rain that I decided to stick a meter stick in the gauge to measure the rain amount, and save pouring into the inner tube for the end of the storm.  The gauge tilts slightly, so I took a measurement on the uptilt side and the downtilt side and calculated an average.   That evening I found that the bottom of the gauge sagged in the middle, leading to an even deeper measurement than the downtilt side.  With these flaws, the lack of the ten-to-one exaggeration of depth, and some measurements being taken in the dark with a flashlight, my data were only approximate. I recorded measurements to within the nearest quarter inch (see the graph below).

Were my measurements accurate? On Friday morning, September 13, I took measurement using a more accurate method to compare with my estimates.  After bailing out five full tubes of rain, I poured the remaining water through the funnel into the tube to a depth of 13.5 inches (343 mm), spilling a little bit during this process.  The result was 0.38 inches (9.5 mm) more than my rough estimate from the night before – a storm total of 14.52 inches (369 mm) up to this time. On the graph, this is marked as 1. (The lower shows the uncorrected values.)

But the rain hadn’t stopped.  I awoke on the morning of September 15^th and heard reports that up to 2 inches (51 mm) of rain fell overnight. I went outside to check our gauge – only to see that it had been knocked over (probably by raccoons).  Fortunately, I have a second rain gauge in my backyard – a plastic gauge that registered about 0.25 inches (6 mm). I added a conservative 0.2 inches (5 mm), since this gauge was under trees (marked as 2 on the graph).

The final number:  16.37 inches (416 mm) of rain, more or less.

The exposure of the rain gauge is undoubtedly the greatest source of error.  According to the National Weather Service and CoCoRAHS (both of which use citizen volunteers to measure rainfall), “exposure” of the rain gauge is important. Rain may be blocked by nearby obstacles causing the number to be lower than it should. Or, rain may be blown into or away from the gauge by wind gusts.  The recommendation is that the gauge be about twice the distance from the height of the nearest obstacles, but still sheltered from the wind.

The gauge was certainly sheltered from the wind.  It is located about 10 feet (~2 meters) south of the house, which is about 15 feet (5 meters) high, and to the west of a fence and small trees as well as the tree in the photograph.   There is a much smaller tree to the southwest.

All the obstacles suggest that some rain could have been blocked from reaching the gauge, which would imply that the rainfall total is too small.  On the other hand, some rain might have been running down the branch in the picture. (In fact, because of the large amount, I thought this might be the main effect before doing some research on exposure)

It is also recommended that the gauge be level, which it wasn’t.  I’m not too worried about this, since it was nearly vertical.

The conclusion?  There was a lot of rain.  It could have been an inch (25 mm) more or less than my measurement. Acknowledging this is called reporting error. It doesn’t mean that the measurements are wrong, it just gives an idea of how accurate they are. My total was not the largest; there were at least two other measurements near 18 inches (457 mm).

Now that I’ve described all that can go wrong measuring rainfall, let me add that, putting a rain gauge in the right place, and taking an accurate rainfall measurement is fairly easy. If you have a perfect cylinder, such as a GLOBE rain gauge, simply stick a ruler in and read the depth (make sure to correct for any offset of the “zero” line and correct for this offset; and see if the ruler pushes the water level up very much).

If you don’t have a rain gauge but have a bucket (or glass) with sides that aren’t straight up and down, you’ll need to do a little math to figure it out. Here’s what you’ll need to do:

1. Measure the diameter of the bucket at the level of the rain.  Subtract out twice the thickness of the walls.
2. Measure the diameter of the bucket at the bottom in the same way.
3. Calculate the average of the two diameters.
4. Divide by two to find the average radius.
5. Find the average volume of rain = Depth x radius x radius x 3.14.
6. Find the area at the top of the bucket (this is the area over which the rain is collected).
   1. Measure the diameter
   2. Divide the diameter by 2 to get the radius
   3. Area = radius x radius x 3.14 (remember that Area = pi x radius²)
7. Divide the rainfall volume by this area to get the rainfall.

It would be an interesting activity to put several buckets (or rain gauges) in different places in a field, your back yard, or your schoolyard to see how much the measurements vary within the area. Soup cans, though not perfect, would work pretty well for the activity, especially if they’re the same size.  I might try this during the next rainstorm.  (I hope not too soon!)

Does your school collect precipitation data? Have you had an extreme weather event that you were able to record? Let us know by adding a comment!